Learning Path for Binomialdistribution

Warning: MathJax requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2/5

2 Zufallsvariablen - das Arbeitspferd der Wahrscheinlichkeitsrechnung

Wenn man bei dem vorigen Urnenbeispiel eine so Art "Mittelwert" bei den Zufallsversuchen berechnen möchte, wird das schwer gehen - wie soll man mit "rot", "weiß" und "schwarz" rechnen. Man hilft sich hier, indem man den Farben (allgemein den Ausfällen) Zahlen zuordnet - ja und mit Zahlen kann man ja wohl rechnen. Dieses "Dings", das diese Zuordnung macht, heißt - ja richtig- Zufallsvariable(ZV) und wird meist mit einem Großbuchstaben bezeichnet - beliebt sind X, Y , Z.
Die Idee ist also, dass jeder Ausfall $\omega \in \Omega$ mit einer reellen Zahl $a_i$(stellen Sie sich einfach vor mit Geld - das passt gut in unsere Zeit) bewertet wird. Z.B.: rot mit 5.2, schwarz mit $\pi$ und weiß mit $\sqrt{2}$. Unser Interesse gilt jetzt nicht mehr den einzelnen Ausfällen, sondern wir schauen uns die möglichen Werte der ZV mit ihren Wahrscheinlichkeiten an - das nennt sich dann Wahrscheinlichkeitsverteilung von X. Das klingt zunächst komplizierter als es ist. Aber zunächst die
Definition einer ZV X \begin{align} X: \Omega & \mapsto W \subseteq \mathbb{R} \\ \omega & \mapsto X(\omega)=a_i \end{align} Wie die Indizierung von den Werten $a_i$ bereits nahelegt, beschäftigen wir uns zunächst mit abzählbaren $\Omega$'s, sodass die Werte $a_i$ endliche oder unendliche Folgen bilden! Die Wahrscheinlichkeitsverteilung von X ist dann die Berechnung aller $P(a_i)$ meist geschrieben als $P(X=a_i$)- meist in Tabellenform.
Beispiel: In einer Urne befinden sich 3 weiße, 2 schwarze und 1 rote Kugel. Es werden 2 Kugeln hintereinander ohne Zurücklegen gezogen. Für jede weiße Kugel gewinnt man 1 Euro, je schwarze 2 Euro und für die rote gibts leider nichts. Wir "basteln" uns eine ZV X, die den Gewinn pro Doppelzug darstellt. Gib die Wahrscheinlichkeitsverteilung von X in einer Tabelle an
Also los gehts: Wir überlegen zuerst alle Möglichkeiten in $\Omega$ und ermitteln die dazugehörigen Werte von X:
\begin{equation} (w,w)\mapsto 2, (w,s)\mapsto 3, (s,s)\mapsto 4, (w,r)\mapsto 1, (s,r)\mapsto 2 \Rightarrow W=\{1,2,3,4\} =\{a_i\} \end{equation} zu diesen Werten suchen wir jetzt die Wahrscheinlichkeiten $P(X=a_i)$

$X$ 1 2 3 4 $\Sigma P(X=a_i)$

$P(X=a_i)$ $\frac{6}{30}$ .... $\frac{12}{30}$ .... ....

1 als Wert der ZV X ist nur möglich mit den Ausfällen (w,r) bzw. (r,w), die W. dafür sind je 3/30, da die Ausfälle unvereinbar sind, darf man einfach addieren, also 6/30.

3 als Wert der ZV X ist nur möglich mit den Ausfällen (w,s) bzw. (s,w), die W. dafür sind je 6/30, da die Ausfälle unvereinbar sind, darf man einfach addieren, also 12/30.

Das Ergebnis für 2 ist (in Dreissigstel - nur mehr Zähler eingeben)

Das Ergebnis für 4 ist (in Dreissigstel - nur mehr Zähler eingeben)

Das Ergebnis für die letzte Spalte (als ganze Zahl) Leider falsch!
Das Ergebnis in der letzten Spalte sollte uns nicht überraschen, denn sei $E_i$ das Ereignis $X=i$, so erfüllen diese Ereignisse den Sachverhalt in der vorigen Lektion \begin{align} \Omega = E_1 \cup E_2 \cup \ldots \cup E_n \qquad und \qquad \forall i,j (i \neq j)\in \{1,2,\ldots n\}: E_i \cap E_j = \{\} \Rightarrow \sum_{i=1}^n P(E_i)=1 \end{align} Man kann also die letzte Spalte als Probe verwenden oder damit eine (schwer) zu berechnende Spalte ermitteln!
In der beschreibenden Statistik gibt es gewisse Kennzahlen von Merkmalen $x_i$, so z.B.: \begin{align} \bar x = \frac{\sum_i H_i \cdot x_i}{\sum_i H_i} = \sum_i h_i \cdot x_i & \qquad \textrm{dabei sind die }H_i \textrm{ die absoluten Häufigkeiten } \\ & \qquad \textrm{und die }h_i \textrm{ die relativen Häufigkeiten } \end{align}

Wie heißt dieses Merkmal
Es ist jetzt leicht die Begriffe Mittelwert und Varianz für eine ZV X zu erweitern - wir ersetzen in den Formeln der Statistik die relativen Häufigkeiten durch die Wahrscheinlichkeiten:
- (1) Erwartungswert der ZV X (in Zeichen E(X)) ist festgelegt: \begin{align} E(X) = \mu = \sum_i P(X=a_i) \cdot a_i \quad \textrm{oder kurz}\quad \mu = \sum_i p_i \cdot a_i \end{align}
- (2) Varianz der ZV X (in Zeichen V(X)) ist festgelegt: \begin{align} V(X) = \sum_i (a_i - \mu)^2 p_i \qquad \sigma = \sqrt{V(X)} \end{align}
- Aus obigen Definitionen lässt sich durch ausquadrieren des Summenterms in (2) zeigen: \begin{align} V(X) = E(X^2) -(E(X))^2 = E(X^2) - \mu^2 = \sum_i p_i \cdot a_i^2 - \mu^2 \end{align}
- Beachte, dass für das praktische Rechnen in wxMaxima E(X) das skalare Produkt von Wertevektor mit Wahrscheinlichkeitsvektor ist. Die Varianz lässt sich mit dem letzten Satz dann ebenfalls als Skalarprodukt des quadratischen Wertevektors([.......]^2) mit dem W-Vektor berechnen(minus E(X)^2).
  Probieren wir das gleich einmal für unser obiges Urnenbeispiel:
  Wie groß ist E(X) als irreduzibler Bruch?
  
  Wie groß ist V(X) als irreduzibler Bruch?
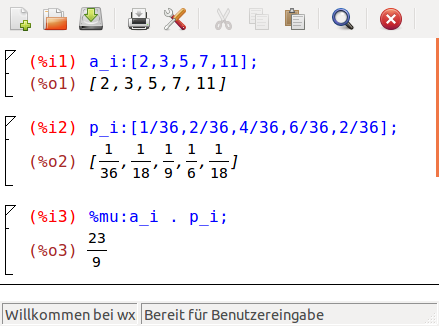
Hier die Berechnung mit wxMaxima (mit dem "Trick" des skalaren Produkts sind keine Summen notwendig!)

Hier die Berechnung mit Calc("nach rechts ausfüllen" verwenden - eh klar!)

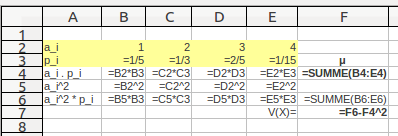
Wie wird die Zahl in Zelle F4 bezeichnet?
Noch ein Beispiel zum "Drüberstreuen": Es wird 2-mal gewürfelt. Ergibt die Ziffersumme eine Primzahl bekommt man diese in Euro, im andern Fall ist der Einsatz "futsch". Wie hoch muss der Einsatz sein, damit das Spiel fair ist?
Wie lautet das Ergebnis als irreduzibler Bruch?

Hier noch die Berechnung als "Zugabe":

Weiter zu Lektion 3